Diversification vs. Diworsification

Can you have too many assets?

Jun 15, 2022

No Episode Next Week

Chemo week starts on Monday and since I was an idiot who decided to write about Uvalde two weeks ago, I’m going to take next week off. Enjoy your downtime where I’m sure you’ll find plenty of other stuff to keep you busy.

Finance? What’s This?

We’ve gone a bit off the rails (which is a good thing) over the last few weeks as we’ve talked about college and Uvalde. I said from the beginning that we would cover a range of topics since this is as much my retirement hobby as anything else. So expect to be sidetracked some more in upcoming weeks, but for now we’re going to return to finance.

Today’s topic is diversification vs. diworsification — can we have too many assets? My quick answer (which applies to all of us without the investing bug) is no. Why, because ideally you will be well diversified across stocks, fixed income, real estate, international, and maybe a little gold (I don’t own any) in ETFs. You’ll adjust for risk tolerance about once a year, take advantage of tax-sheltered savings plans, and save regularly. In 30-35 years, you’ll ride off into the retirement sunset and never spend more than an hour or so a year on your investment decisions. This will leave you plenty of time to pursue reading, going for a walk, gardening (too many bugs and weeds for me), playing with your kids, or any of the other hobbies that are more fun to most people.

For people who were dropped on their heads as small children, you might find investing interesting (and yep, I’m in this club). If so, let’s see if we can find a small edge (which evidence suggests is less likely than we’d like to believe) which actually would make it worth doing.

Academic Time

Feel free to skip this section if you’ve already got a good grasp on it. It is not reinventing the wheel, merely pulling up expected return, standard deviation, correlation and bringing us up to speed on the what we mean by diversification. I’ve covered this a bit before, but we’ve got some new readers since then.

Expected Return

The expected return is merely the average return we are going to earn over a specific holding period. While it is typically introduced as a probability distribution, that is a poor way to look at it because it assumes we know (a) the probability of each event and (b) the outcome of that event. The reality is that we don’t know either one. That said, let’s go through a quick example.

In this example, the expected return is 9.0% and the standard deviation is 18.28%.1

Then we move onto the expected return and standard deviation of a portfolio which gets a little more complicated for the standard deviation. This is because we need to assume that our assets may be correlated.

Correlation

What do we mean by correlated? Correlation refers to the rate of linear relationship (we’ll come back to this) between one variable and the other. So, if we are looking at two stocks (let’s call them A and B) and every time stock A is up, B is typically up as well, we have positive correlation. If every time stock A is up, B usually moves in the opposite direction, we have negative correlation. Finally, if every time A is up, B may be down or may be up (there is no relationship), we have 0 correlation. Correlations can not exceed 1.0 (perfect positive correlation) or fall below -1.0 (perfect negative correlation), but rarely will you ever see a correlation of 1.0 or -1.0. Even if you take a look at companies in the same industry (such as oil and gas), the correlations between BP and Exxon (on weekly data over the past 5 years) is 0.77. Here you can see some correlations through 2020.

Correlations And St Deviations 2021 Edit2

151KB ∙ XLSX file

Download

Note that most correlations are weakly positive (due primarily to general economic factors like inflation, GDP growth, tax rates, etc.) but lowered dramatically by firm-specific factors (factors impacting Amazon are likely very different than those impacting Exxon). Therefore, the average correlation is probably going to be in the 0.20 - 0.35 ballpark. If you look at the “Handout” sheet in cells B60 and B61, you’ll see the average correlation across all securities (0.29) and the average correlation for firms in the same industry (such as BP and Exxon at 0.52).

Expected Return and Standard Deviation of a Portfolio

When looking at a two-stock portfolio, we get the following formulas.

If we have Stock A with a 9% expected return and 25% standard deviation and add Stock B with a 9% expected return and 25% standard deviation in a 50/50 mix, the portfolio standard deviation will be BELOW 25% — with no reduction in the expected return. This is the free lunch of diversification. For example, assume the stocks have a correlation of 0.3. Then, the expected return will be 9% and the standard deviation will only be 20.16%.2 As mentioned earlier, it is really stupid to only own two assets as many people hold portfolios of assets. Therefore, you can expand the standard deviation of the portfolio formula like this (where Cov stands for Covariance)

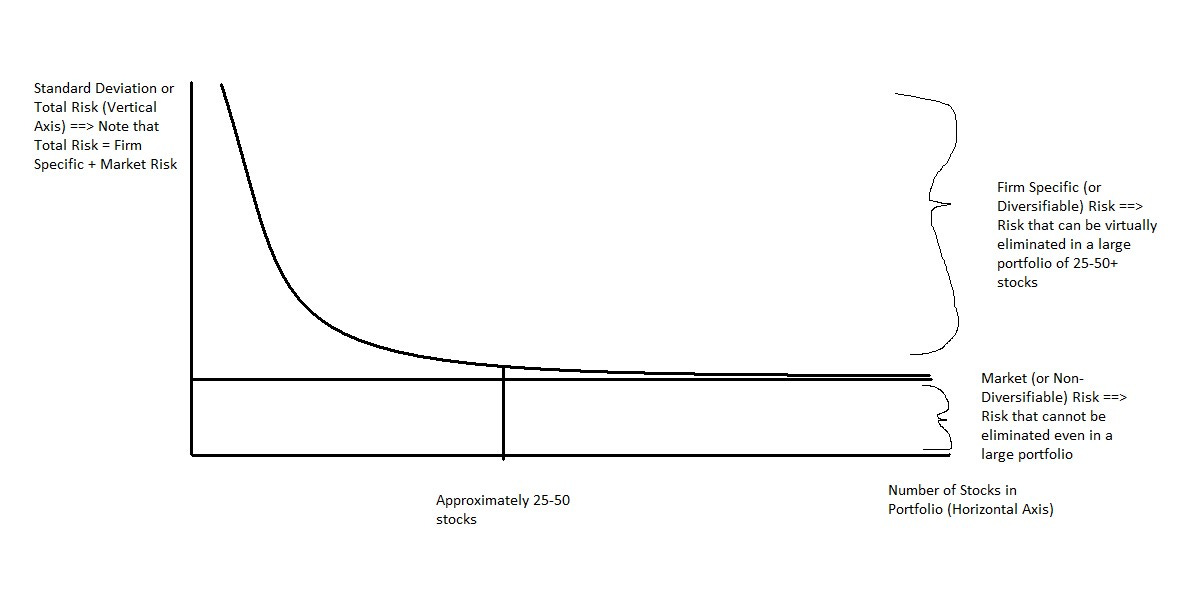
Ultimately, this will give you a standard deviation mix that looks like this (with a large group of assets to create random 1-asset, 2-asset, 3-asset, 4-asset, etc. portfolios).

So, the standard story on diversification is that if we combine assets (the graph refers to stocks, but better to think of assets) in a portfolio, we greatly reduce the firm-specific risk until there is only market risk left over. Thus, going from 1 asset to 5 assets has a big impact on reducing our firm-specific risk. Going from 5 assets to 15 assets is also going to have a big impact on reducing our firm-specific risk. but likely a little less than going from 1 to 5. However, going from 130 assets to 150 assets, is probably going to barely move the needle as we have eliminated most of our firm-specific risk already when we held 130 assets. Think of a situation were you go from owning just Microsoft to dividing the portfolio into Microsoft, Exxon, Target, Ford, and Moderna. We went from one stock (if Microsoft disappoints our portfolio tanks) to owning 5 stocks. Now, if Microsoft only represents 20% of our portfolio and reports bad results, we’ll still feel it. However, much less so when Exxon, Target, Ford, and Moderna are not reporting the same bad news. However, if inflation goes up, that’s going to impact all the companies (not necessarily to the same extent). Now imagine you own Microsoft and 99 other companies. Even if Microsoft declares bankruptcy tomorrow, you still have 99 other companies to offset it. Essentially, Microsoft goes from 100% of your portfolio to 20% of your portfolio and then down to 1% of your portfolio. Clearly, the impact of what happens to Microsoft is going down dramatically as we add more stocks to the portfolio, but at a decreasing rate.

We’ll end the academic portion here and jump back into the real world where things are always quite a bit more messy than we want to believe.

Historical Data Doesn’t Imply Future Data

Some parts of historical data are more reliable than others. We have historical returns (which are not 100% worthless, but probably close), historical variance (which is more reliable) and correlations (which are reasonably reliable, but are going to tend to move towards historical norms). Look at the data in the 5-year returns for some of these companies along with what’s happened since 2021.

Returns are very unpredictable
Standard Deviations are more predictable (maybe the most predictable)
Correlations are likely to stay high (within industry) or move toward the mean (out of industry)

Unfortunately, changing the returns will greatly throw off any optimization attempts regardless of how well standard deviation and (to an extent) correlation track. Also, while standard deviations do tend to be much more predictable, correlations will move towards the average for the mean. Granted, this is a REALLY small sample size (too small to be meaningful beyond merely observation). However, it is using actual data from real companies and I selected the data in early 2021 to make the original spreadsheet. The return data is since that time. We can probably use other tools to estimate required returns and correlations while using historical data for returns which will help quite a bit. Yet, the “optimal portfolio” over a previous period is not going to be the “optimal portfolio” over the upcoming period. This is due to your three inputs (return, standard deviation, and correlation) changing.

Companies Evolve (Up and Down)

Let’s look at Meta (aka Facebook). It has gone from a basic social media company to a company with Instagram, Whatsapp, Oculus and is trying to create the metaverse (along with several other competing companies). The company that came public in 2012 is not the same company that is competing today. Therefore, we need to take a look not at what has been, but what we expect to be over the next few years.

Some restaurants thrived in the shutdowns of COVID (such as Chipotle) and others closed down because they weren’t designed to operate in a digital ordering process. Walmart did not do deliveries, but they do now. Peloton suffered from COVID (in a classic pull ahead move that many didn’t fully recognize) as people ordered bikes and signed up, only to get tired of them a year or so later. Companies evolve up and down over time and our goal as analysts are to forecast these changes.

This is easy in hindsight, but MUCH, MUCH more difficult to do in real time as the changes come very quickly and from a lot of directions. Don’t think in terms of “this will happen”. Instead, think in terms of probabilities (again, much more difficult to do in practice as our mind wipes probabilities away pretty quickly). Keep a journal and write down what you think is going to happen, when it is going to happen, and how likely it is going to happen. It will be ugly, but the only way to improve is to know how far off and in what direction you were.

Share Kevin’s Newsletter

Jump Back to mid-2019

Let’s take a short trip in time back three years. How likely did you predict COVID, Federal Stimulus throughout COVID, January 6th, Ukraine-Russia, high inflation, or any other of the big events that occured. I’m guessing you assigned pretty close to a 0 probability on any of these events (heck, things like COVID weren’t even on your radar). Yet, they turned out to be defining events (definitely not the only key events) over the past three years. Each of these impacted the expected return, standard deviation, and correlation of your securities, but was likely way off your radar. Which means what things THAT YOU ARE NOT THINKING ABOUT now are likely to impact your forecasts? Something that you may try is to add to your investing journal what things are not currently on your radar (even if unlikely) may have a big impact on the expected return, standard deviation and correlation of your investments.

Correlation Can Be Messy

We use correlation to tell us how closely two variables move together in a linear manner. Which usually works fine, but can also be messy because there may be reasons why they don’t move in a linear fashion. Consider the following correlation tables and you can see examples where correlation can be misleading.

We often think of correlation along the lines of the top set of examples. However, if you look at the bottom set, you’ll see that correlation implies how closely the variables move together in a linear fashion. Now, it is typical to see examples like the first row (well, not really 1 or -1, but we often see data between 0.8 and -0.2. Remember that if your past observation was estimated to be -0.2, it is probably more likely to be a data artifact and the real correlation is likely going to be in the 0.2 - 0.3 range. If your correlation was in the higher end, it is likely to be in the same industry or a data artifact as well.

Can You Have Too Many Assets?

The answer is both yes and no. If you have the ability to make some meaningful predictions that turn out (on average…no one is getting every pick right) correct, then yes. You don’t want to own Peloton as it plummets from $165 back in early 2021 to $10.50 today or Shopify as it goes from $1700 to $350. These are some ugly routes that would be nice to avoid. However, and I can not stress this enough, it is easy to call Peloton too expensive at $165 after it is down to $10.50. It is far more challenging to think that it was actually worth $10.50 when it was trading for $165. When it fell to $100, did you think it had fallen far enough? How about when it hit $50? By far more challenging, I mean that no one did (at least not publicly). How about Bitcoin at $65,000 (now around $23,500) or some of my holdings (Amazon, FIGS, Facebook, and more)?

Don’t assume that you would have made the prediction that AMC was undervalued when it went from $2.18 on January 14th, 2021 to $20.36 on January 27th, 2021. That is an 833% return in two weeks! Then, the next day it closed at $8.63 for a drop of 58%. Perfectly normal, amirite? On June 2nd, 2021, it hit it’s high of $72.62, up about 3231% in 6 months (that is NOT a typo!). Today, it’s back down to $11.50. What the heck was happening? If you take out the escalator ride, how did a company that was on the verge of bankruptcy end up being up by 420% in just under 18 months? The answer lies in the ability to raise capital once the shares were higher.

Notice what happened during 2021. AMC raised as much capital by issuing 11.55 million shares for $50.86 — over 140% more than it raised by issuing 4.3 times as many shares (50 million) on January 25. The power of reflexivity in action.

Conclusion

Yes, you can have too many assets if they are not a part of your optimal portfolio. In other words, if you don’t have an edge in predicting expected return, standard deviation, and correlation over time. It’s like assuming because you understand the basic rules of poker, you’re going to win the World Series of Poker. Guess what? 90% of the people playing are in the same position (I’m sure there are a few suckers, but fewer than you’d hope)! The problem is figuring out what exactly IS your optimal portfolio because yours will be different from mine. It will depend on how active you want to be. Do you want to make a bet on energy? You can do that with ETFs, but then what happens if you overweight energy and it earns below market returns or has a much higher standard deviation?

If you want peace of mind, own a truly diversified portfolio in tax-sheltered accounts and add to it for 35 years. If you want to dive into the twirling waters of madness (and I’m there with you to an extent) known as investing, be prepared to get wet! Just recognize that you are likely going to learn a lot more, rather than earn a lot more.

Kevin’s Newsletter